Scilab

Scilab
Scilab 4.0
Desarrollador:	Scilab Consortium
Última versión:	4.1.2 (5 de Noviembre de 2007)
S.O.:	Multiplataforma
Género:	Computación Numérica
Licencia:	Licencia SCILAB
En español:	no
Sitio Web:	www.scilab.org

Scilab es un lenguaje de programación de alto nivel para cálculo científico, interactivo de libre uso y disponible en múltiples sistemas operativos (Unix, GNU/Linux, Windows, Solaris, Alpha) desarrolado por INRIA (Institut National de Recherche en Informatique et Automatique) y la ENPC (École Nationale des Ponts et Chaussées) desde 1990. Scilab fue creado para hacer cálculos numéricos aunque también ofrece la posibilidad de hacer algunos cálculos simbólicos como derivadas de funciones polinomiales y racionales. Posee cientos de funciones matemáticas y la posibilidad de integrar programas en los lenguajes más usados (FORTRAN, Java y C y C++ ). Scilab fue hecho para ser un sistema abierto donde el usuario puede definir nuevos tipos de datos y operaciones entre los mismos.

Scilab viene con numerosas herramientas: Gráficos 2-D y 3-D, animación, Álgebra lineal, matrices dispersas, Polinomios y funciones racionales, Simulación: programas de resolución de sistemas de ecuaciones diferenciales (explícitas e implícitas), Scicos: simulador por diagramas en bloque de sistemas dinámicos híbridos, Control clásico, robusto, optimización LMI, Optimización diferenciable y no diferenciable, Tratamiento de señales, Grafos y redes, Scilab paralelo empleando PVM, Estadísticas, Interfase con el cálculo simbólico (Maple, MuPAD), Interfase con TCL/TK

Además se pueden agregar numerosas herramientas o toolboxes hechas por los usuarios como Grocer una herramienta para Econometría u Open FEM (Una caja de Herramientas para Elementos Finitos), hecha por INRIA.

Instalación

Windows

La instalación de Scilab es relativamente sencilla en el entorno Windows. Para hacerla basta con descargar el archivo scilab-4.1.2.exe (aproximadamente 16 Mb en su versión 4.1.2), que esta disponible en la página del proyecto y correrlo. Se siguen unas instrucciones sencillas y se puede ejecutar el programa por medio de un acceso directo.

GNU/Linux

Ubuntu (Distribucion GNU/Linux) [editar]

La instalación de Scilab en Ubuntu se puede realizar de varias formas: Una de estas es buscando el programa en Gestor de paquetes Synaptic desde el menú Sistema>Administración. Se instalará la última versión al seleccionar el programa para instalar aplicar cambios.

Otra forma de instalación es desde la consola (Accesorios>Terminal) dar los comandos para que se descargue la última versión desde los repositorios. Para ejecutar lo anterior se pueden usar los siguientes comandos en la consola o terminal:

sudo apt-get install scilab

o alternativamente:

sudo aptitude install scilab

Se pide la contraseña del usuario y se procede a descargar los paquetes. El programa se instala automáticamente.

Caracteres con significado especial

Scilab al igual que otros programas de análisis numérico tiene caracteres con significado especial que se utilizan para un fin especifico. Por ejemplo al poner dos signos de división (//) el programa lo interpreta como un comentario. Este comando es útil al realizar programas desde SciPad.

El programa además cuenta con constantes definidas como %pi para la constante matemática $π$ . La siguiente tabla resume los caracteres de uso especial del programa:

Gráficos

Gráficos en 2d

Gráfico de la función $y = f (x) = s e n (t)$

t=[0:0.001:2*%pi]
y=sin(t)
plot(t,y)

Gráficos 3d

Gráfico de una función de dos variables $z=f(x,y)=x^2-y^2+xcdot y-1$

x=[-10:0.5:10];//El dominio en el que se va a evaluar la función es el plano x entre -10 y 10, con intervalos de 0.5
y=[-10:0.5:10];//El dominio en el que se va a evaluar la función es el plano y entre -10 y 10, con intervalos de 0.5
[u,v]=meshgrid(x,y); //Se define una matriz auxiliar para "x" y "y" con el fin de evaluar la función
z=u.^2-v.^2+u.*v-1;//Se evalúa la función. Notese los puntos para que Scilab no interprete producto de matrices si no valor a valor
plot3d(x,y,z)

Se pueden ver las líneas de nivel de la función por medio del siguiente comando:

contour(x,y,z,10)

El número 10 indica el número de curvas de nivel que debe mostrar el programa.

Matrices

Scilab permite la operación de matrices. La matrices se pueden introducir insertando reglón por reglón, separando las columnas por un espacio y para cambiar de reglón poniendo un punto y coma. Por ejemplo para introducir la siguiente matriz:

$A = begin{bmatrix} frac{2}{3} & frac{3}{5} \ 21 & 7 \ end{bmatrix}$

se pueden utilizar los siguientes comandos:

A=[2/3 3/5; 21 7];

quedando la matriz guardada en la variable A.

Scilab realiza operaciones sobre las matrices, como la inversa, el determinante, suma y multiplicaciones.

Para hallar la inversa de una matriz se utiliza el comando inv(A). El determinante se calcula con el comando det(A).

Programas

Este el tradicional programa Hello World hecho en Scilab

//línea de comentario.... como en C++
clc
//limpia la pantalla
disp("Hola Mundo")
//imprime Hola Mundo

Este programa integra numéricamente el sistema de ecuaciones diferenciales conocido como Oscilador de van der Pol:

$dot x=y$

$dot y=-x+y(1-x^2)$

Lo primero es crear una función que de cuenta de las anteriores ecuaciones (es decir que al ingresarle $x$ , $y$ y $t$ esta devuelva 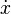$dot x$ y $dot y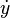$ ) esta puede crearse con SciPad y se puede guardar con el nombre de vdp.sci y contiene lo siguiente:

function fxy =vdp(x,y)
fxy=zeros(2,1)
fxy(1)=y(2)
fxy(2)=-y(1)+y(2)*(1-y(1)*y(1))
endfunction

Luego se ejecuta el siguiente script que usa la función anteriormente creada, invoca a la función ode de scilab y finalmente muestra la gráfica (que hace parte de la imagen mostrada en esta página):

getf vdp.sci
x0=0.01;
y0=[0.00001;0.00001];
t=[0.01:0.01:5000*0.01];
yt=ode(y0,x0,t,vdp);
x=yt(1,:);
y=yt(2,:);
plot2d(x,y,2)

Polinomios y calculo simbólico

Scilab tiene funciones diseñadas especialmente para el tratamiento de polinomios y calculo simbólico (aunque existen otros que facilitan la transcripción de texto como Maxima). Por ejemplo para insertar el polinomio:

$y=f(x)=5cdot x^3+frac{1}{2}cdot x-3$

Se utilizan los siguientes comandos (notese que los coeficientes del polinomio se insertan del termino con menor orden $x 0$ hasta el termino de orden mayor $x 3$ poniendo ceros en los términos no existentes:

y=poly([-3 1/2 0 5],"x","coeff")

Para hallar las raices de un polinomio dado, se utiliza el comando roots que se emplea de la siguiente forma:

s=roots(poly([-3 1/2 0 5],"x","coeff"))

o si ya se tiene definido un polinomio (en el ejemplo se ha definido como y')':

s=roots(y)

El vector s guarda las raíces del polinomio, sean estas reales o complejas.

Se pueden hacer operaciones simbólicas entre los polinomios. Por ejemplo si se quiere hacer la siguiente operación:

$z=((x+1)cdot (x-1))^2=(x^2-1)^2=x^4-2cdot x^2+1$

podemos proceder con las siguientes ordenes:

p1=poly([1 1],"x","coeff");
p2=poly([-1 1],"x","coeff");
oper1=p1*p2
oper2=oper1^2

Si se desea evaluar el anterior polinomio en un punto determinado y guardar su valor en una variable f, se pueden utilizar los siguientes comandos:

f=horner(oper2,3)

Notese que se ha evaluado el polinomio en el punto x=3.

Estos procedimientos sirven y funcionan de igual forma para funciones racionales, lo cual es muy útil en la teoría de control. Por ejemplo se puede obtener el producto (la suma, la diferencia o el cociente) de dos funciones definidas como siguen:

$G(bold{s})=frac{bold{s}}{bold{s}^2+1}$ ; $H(bold{s})=frac{1}{bold{s}}$
$G(bold{s})cdot H(bold{s})=frac{1}{bold{s}^2+1}$

Lo que en Scilab se realiza de la siguiente forma (notese la forma de definir las funciones, de forma similar como se hace en Matlab:

s=poly(0,"s")// se define la variable s como un polinomio de orden 1
g=s/(s^2+1)
h=1/s
gh=g*h

Los polinomios se pueden declarar también por sus raíces no incluyendo la opción "coeff" en el comando "poly", como se hizo en el ejemplo anterior al definir $bold{s}$ como un polinomio con raíz en cero.

Fracciones parciales

El programa también tiene opciones para calculo simbólico. Por ejemplo, sí se tiene la siguiente función racional:

$G(s)=frac{s^2}{(s+1)^3-2}$

puede ser introducida por los siguientes comandos:

s=poly(0,"s");
g=s^2/((s+1)^3-2);

El numerador y el denominador de la función $G (s)$ puede ser recuperado en variables mediante los siguientes comandos:

numerador=numer(g)
denominador=denom(g)

Scicos

El programa Scilab tiene un entorno similar a Simulink de Matlab para simulación de sistemas dinámicos y resolución de sistemas de ecuaciones diferenciales. Este entorno posee varios paquetes que incluye algunas herramientas para simulación sencilla de circuitos eléctricos y termo hidráulica.

Para lanzar el entorno desde Scilab basta con poner el siguiente comando:

scicos;

Se lanza una nueva ventana, desde en la cual se insertan y conectan todos los bloques ha voluntad del usuario.

Paquetes disponibles para Scilab (Toolbox)

Programas similares

Enlaces externos

Página Oficial de Scilab
Introducción a Scilab (PDF) Es un manual básico escrito en español, con ejemplos claros y fáciles de aplicar
eBook "Basics on digital controller with scilab/scicos (FREE Download)